The Levi-Civita Connection | SpringerLink
International Conference on Riemannian Geometry ICRG on January 14-15, 2022 in Zurich, Switzerland
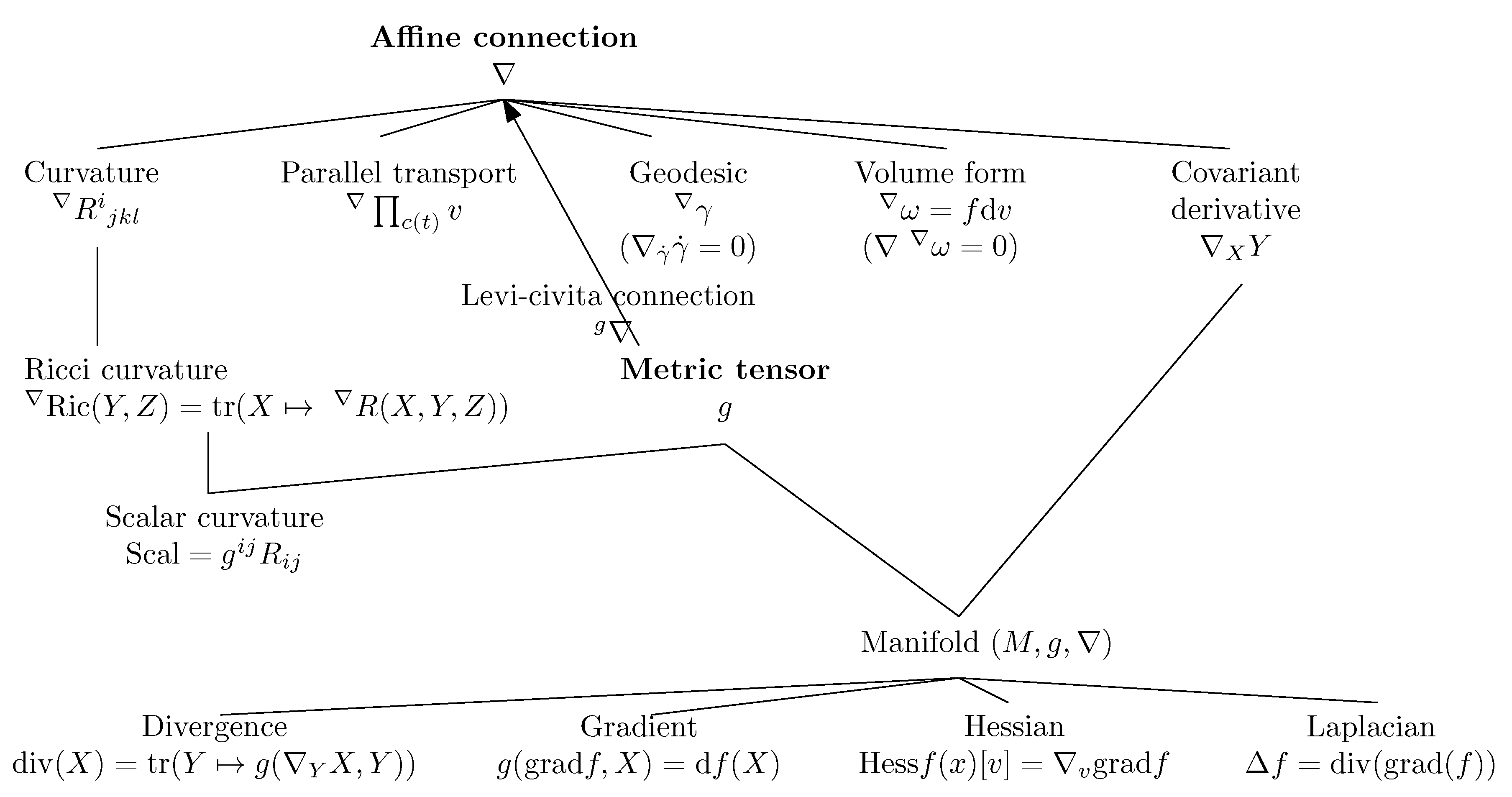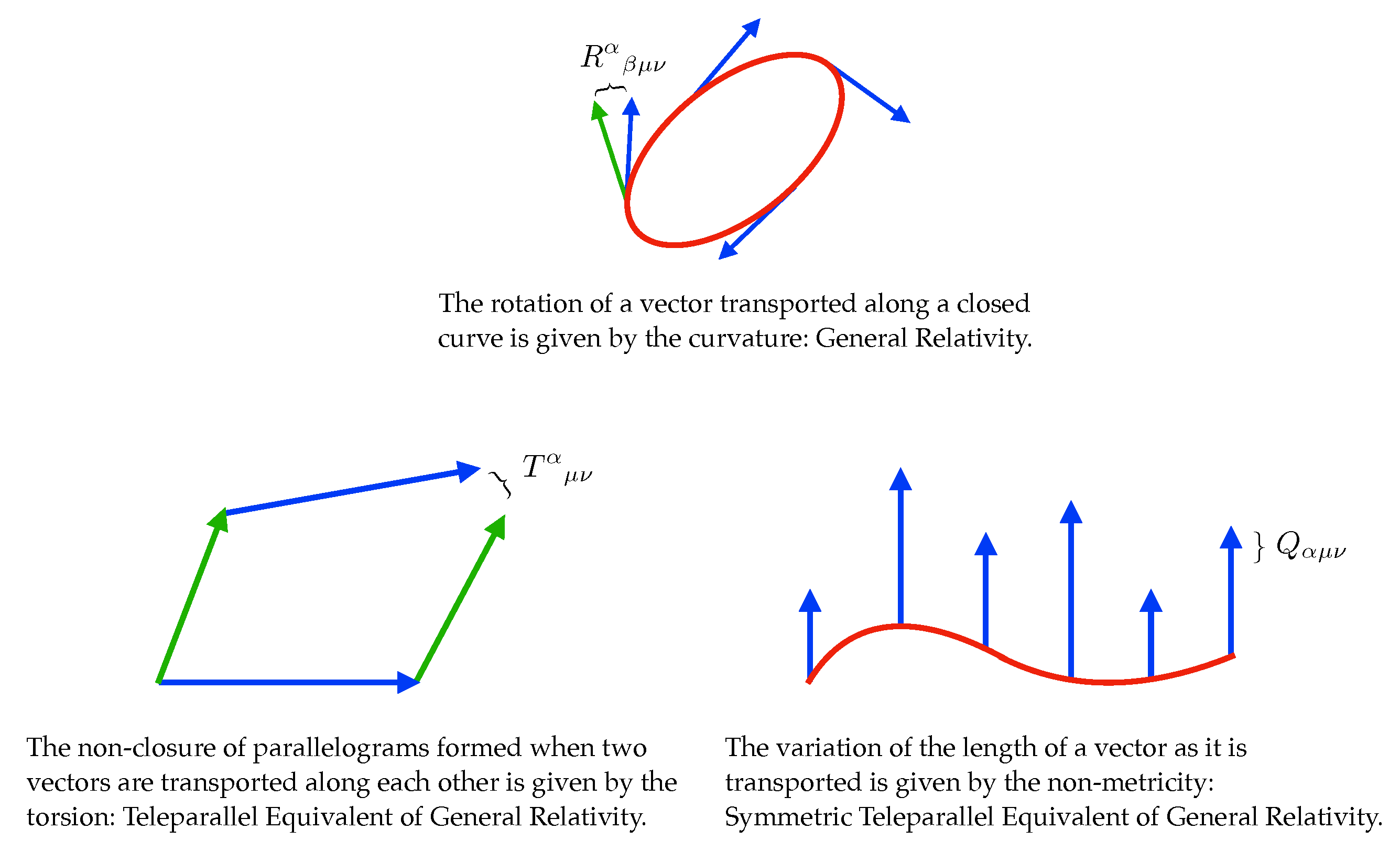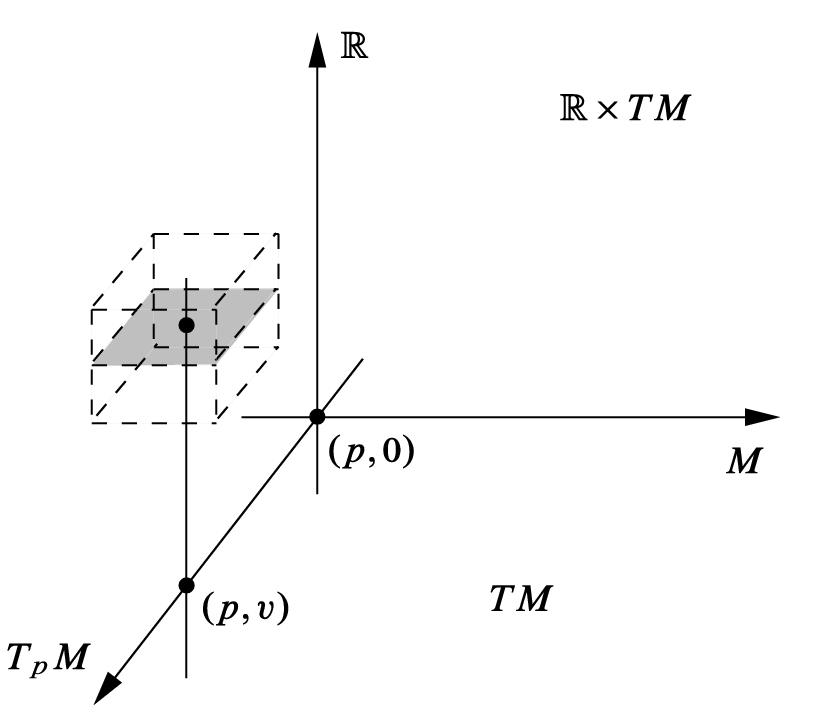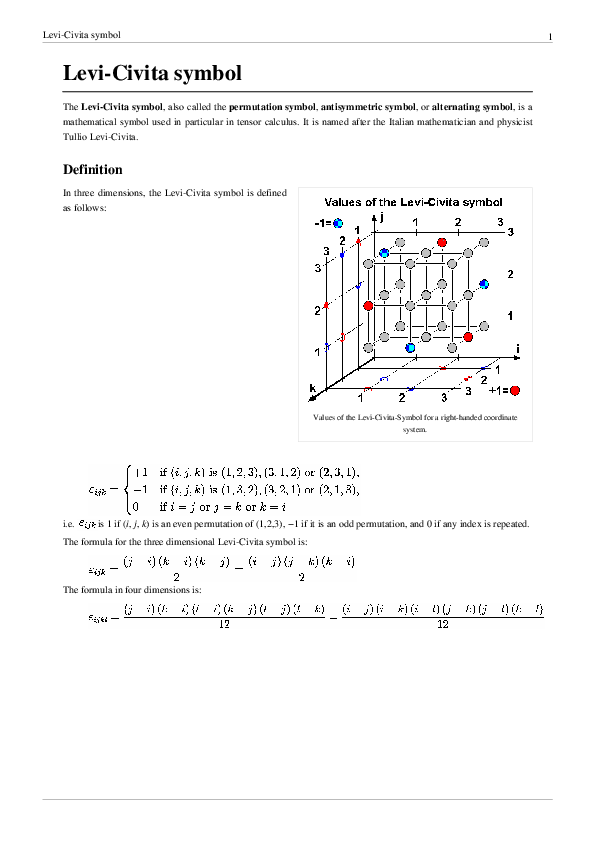
Sensors | Free Full-Text | A Literature Review: Geometric Methods and Their Applications in Human-Related Analysis | HTML
Elementary Differential Geometry | SpringerLink
Entropy | Free Full-Text | An Elementary Introduction to Information Geometry | HTML
Universe | Free Full-Text | The Geometrical Trinity of Gravity | HTML
PDF) On Nearly-Kähler Geometry
The Levi-Civita Connection | SpringerLink
The Levi-Civita Connection | SpringerLink
Second order parallel tensors on singular quasi-constant curvature manifolds | Request PDF
The Levi-Civita Connection | SpringerLink
Some Estimates Over Spacelike Spin Hypersurfaces of Lorentzian Manifold | Request PDF
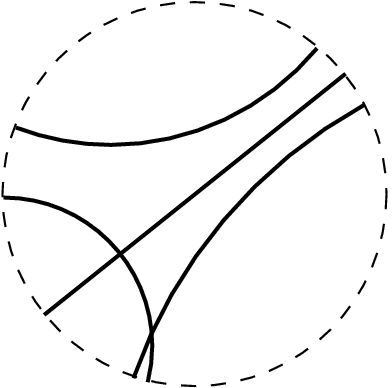
Frank Nielsen on Twitter: "Geodesics=“straight lines” wrt affine connection, = locally minimizing length curves when the connection is the metric Levi-Civita connection. Two ways to define geodesics: Initial Values or Boundary Values.
Chapter 6 Riemannian Manifolds and Connections
Levi-Civita and Nunes transport of a vector v 0 satarting at p through | Download Scientific Diagram
Tullio Levi-Civita - Wikiwand
The Levi-Civita Connection | SpringerLink
On a special type of Riemannian manifold admitting a type of semi ...
PDF) Levi-Civita symbol | Paul Muljadi - Academia.edu
Pseudo-Riemannian geometry encodes information geometry in optimal transport | SpringerLink
Levi-Civita symbol - Wikipedia
Levi-Civita connection - Wikipedia
Tullio Levi-Civita - Wikipedia
Introduction to Riemannian Manifolds | SpringerLink
On Magnetic Curves in Almost Cosymplectic Sol Space | Request PDF
